Analytische Geometrie von Geraden und Ebenen
In diesem Abschnitt wollen wir ein paar grundlegende Begriffe aus der Analytischen Geometrie behandeln. Im Vordergrund stehen verschiedene Darstellungen von Geraden und Ebenen.
Darstellungen von Geraden
Jede Gerade in der x1,x2-Ebene lässt sich durch eine Koordinatengleichung
der Form ax1+bx2+c=0 beschreiben.
Punktprobe
Liegt der Punkt A=(0,3) auf der Geraden g mit g:x1+2x2=6
(0,3) in Gleichung einsetzen
Man erhält: 0+2⋅3=6
Damit liegt der Punkt A=(0,3) auf der Geraden.
Koordinatengleichung
Die zwei Punkte P1=(0,1) und P2=(2,0) legen eine Gerade in der Ebene R2 fest.
Setzt man die beiden Punkte in die Parametergleichung der Geraden ein, erhält man das folgende Gleichungssystem
a·0+b·1+c=0a·2+b·0+c=0
Wählt man c=−2 erhält man a=1 und b=2
Vektorielle Punkt-Richtungsform, Parameterform
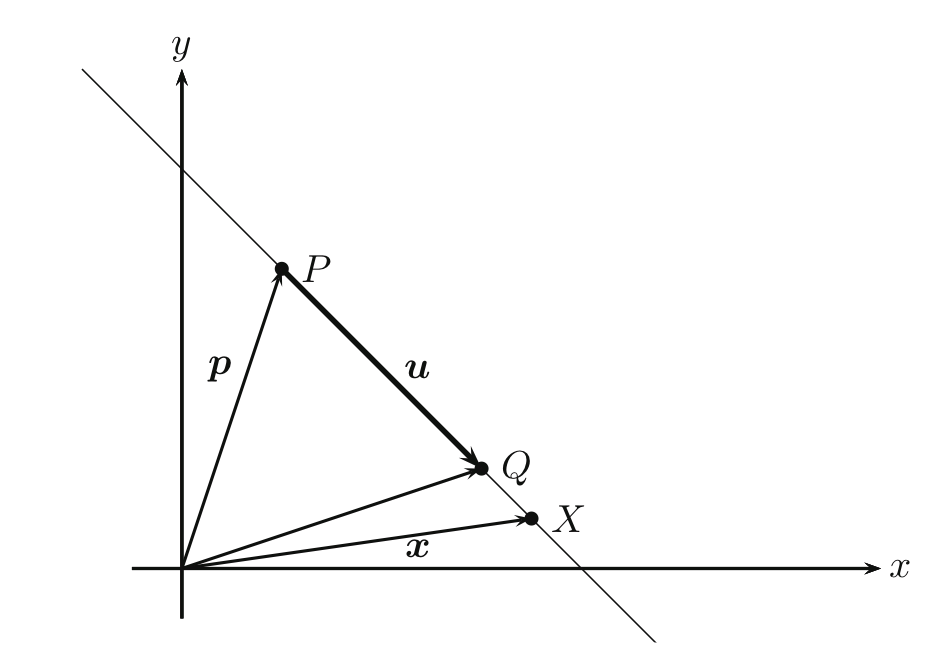
Jede Gerade in der Ebene oder im Raum lässt sich durch eine Gleichung der Form
→x=→p+t⋅→u mit t∈R beschreiben.
Geradengleichung in Parameterform (Parametergleichung)
Aufgabe
Geben Sie zwei Parametergleichungen für die Gerade an, die durch die Punkte A = (1,−2,5) und B = (4,6,−2) geht.
Aufgabe
Prüfen Sie, ob der Punkt A=(−7,−5,8) auf der Geraden liegt, die durch die Gleichung →x=(3−12)+t(52−3) beschrieben ist.
Gleichungssystem
(−7−58)=(3−12)+t(52−3)
Für t=−2 ist jede Zeile des Gleichungssystems erfüllt, damit liegt A auf der Gerade
-
Parameterform → Koordinatenform
Bestimmen Sie die Koordinatenform von der Geraden g
→x=(40)+t⋅(−21)
Lösung
x1=4+t⋅(−2)x2=t
x1=4+x2⋅(−2)
x1+2x2−4=0
Darstellung von Ebenen
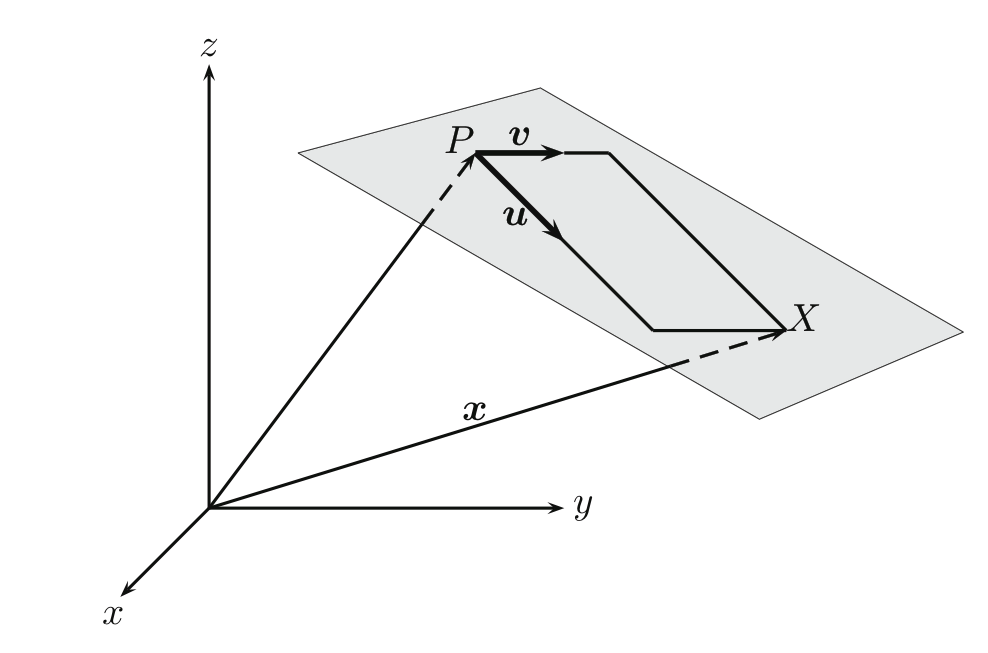
Jede Ebene lässt sich durch eine Gleichung der Form
→x=→p+s⋅→u+t⋅→v mit s,t∈R
beschreiben. Hierbei ist →p der Stützvektor und die nicht parallelen Vektoren →u und →v sind zwei Spannvektoren.
Ebenengleichung in Parameterform
Aufgabe
Die drei Punkte A=(1,−1,1),B=(1.5,1,0) und C=(0,1,1) legen eine Ebene fest. Geben Sie eine Parameterdarstellung dieser Ebene an.
Lösung
Wählt man als Stützvektor den Ortsvektor von A und als Spannvektoren →AB und →AC, so erhält man
→x=(1−11)+s(0.52−1)+t(−120)
Parameterform → Koordinatenform
→x=(111)+s(210)+t(300.5)
Lösung über Gleichungssystem
x1=1+2s+3tx2=1+s+0tx3=1+0s+0.5t
x1=1+2s+3ts=x2−1t=2x3−2
x1=1+2(x2−1)+3(2x3−2)x1=1+2x2−2+6x3−6x1−2x2−6x3+7=0
Koordinatenform → Parameterform
Bestimmen Sie eine Parametergleichung von der Ebene, die durch die Gleichung
3x1−x2+7x3−12=0 gegeben ist.
Lösung
- Schritt auflösen nach einer Koordinaten
x2=3x1+7x3−12
x1=1x1+0x3+0x2=3x1+7x3−12x3=0x1+1x3+0
→x=s⋅(130)+t⋅(071)+(0−120)
Aufgabe
Die drei Punkte A = (1,1,0), B = (1,0,1) und C = (0,1,1) legen eine Ebene fest. Bestimmen Sie eine Koordinatengleichung dieser Ebene.
Lösung
Ansatz: ax1+bx2+cx3+d=0
(1,1,0): a⋅1+b⋅1+c⋅0+d=0(1,0,1): a⋅1+b⋅0+c⋅1+d=0(0,1,1): a⋅0+b⋅1+c⋅1+d=0
Dieses lin Gleichungssystem hat drei Gleicungen und 4 Variablen
(1,1,0): a+b+d=0(1,0,1): −c−d=a(0,1,1): −c−d=b
−c−d−c−d+d=0
c=−12d
(1,0,1): −c−d=a−12d−d=aa=−12d
(0,1,1): −c−d=b−12d−d=bb=−12d
Setzt man d=−2 erhält man a=1,b=1,c=1
x1+x2+x3−2=0
Ebenengleichung in Normalenform
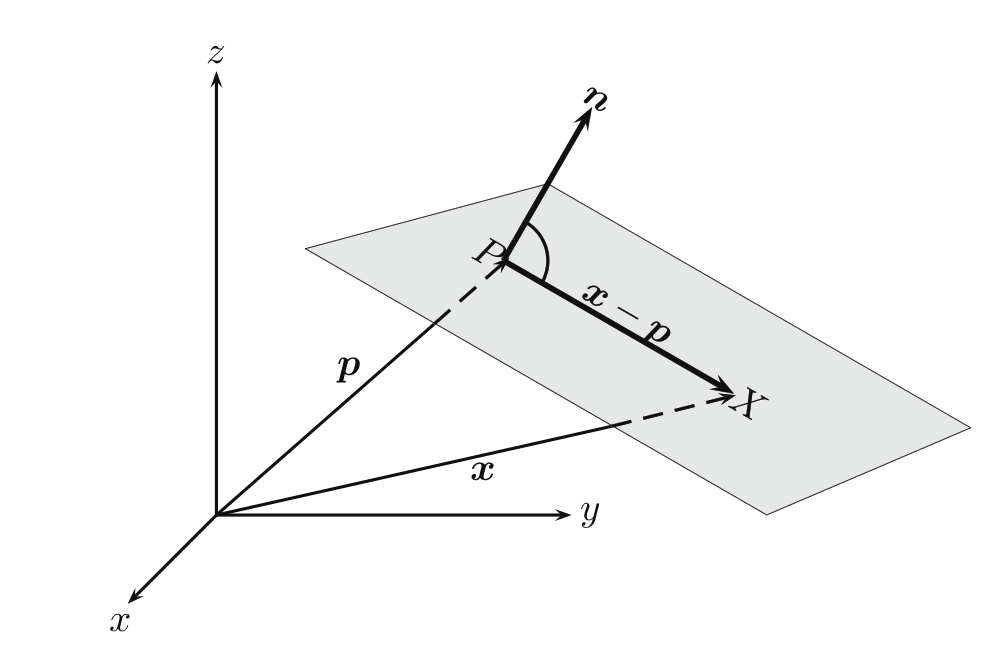
Eine Ebene kann durch einen Stützvektor und einen Normalvektor der Ebene beschrieben werden.
Ein Punkt X liegt genau dann auf der Ebene, wenn der Vektor→x−→p orthogonal zu →n ist. Daher ist (→x−→p)⋅→n=0 eine Gleichung der Ebene.
Koordinatengleichung → Normalform einer Ebene
ax1+bx2+cx3+d=0
(abc)⋅(x1x2x3)+d=0
Normalenform → Koordinatenform
Eine Ebene durch P=(4,1,3) hat den Normalenvektor →n=(2,−1,5)
Lösung
(→x−(413))⋅(2−15)=0
→x⋅(2−15)−(413)⋅(2−15)=0
Lösung
→x⋅(2−15)−(413)⋅(2−15)=0
2x1−x2+5x3−22=0
Koordinatenform → Normalenform
Bestimmen Sie für die Ebene mit der Koordinatengleichung 2x1+5x2+3x3−12=0 eine Ebenengleichung in Normalenform.
Lösung
Zur Bestimmung des Stützvektors →p ist es geschickt, zwei Koordinaten als Null zu wählen
2x1+5x2+3x3−12=0
x2=0,x3=0 dann ist 2x1=12
und
→p=(600)
Lösung
(→x−(600))⋅(253)=0
Ist ax1+bx2+cx3+d=0 eine Koordinatengleichung einer Ebene, so ist der Vektor mit den Koordinaten a,b,c ein Normalenvektor der Ebene.
Aufgabe: Parameterform → Normalenform
Bestimmen Sie für die Ebene in Parameterform
→x=(523)+s⋅(102)+t⋅(0−58)
Lösung
Mit p=(5,2,3) haben wir bereits einen geeigneten Stützvektor.
Der gesuchte Normalvektor muss normal zu beiden Spannvektoren sein.
(n1n2n3)⋅(102)=0
und
(n1n2n3)⋅(0−58)=0
Lösung
n1+2n3=0−5n2+8n3=0
n1=−2n3n2=85n3
Lösung
Wählt man zum Beispiel n3=5
so erhält man
→n=(−1085)
(→x−(523))⋅(−1085)=0