Eine interaktive Lösung des Fermat-Weber Problems mit GeoGebra
P. Fermat stellte im siebzehnten Jahrhundert dem Italienischen Physiker E. Torricelli das folgenden Problem: „Wo befindet sich ein Punkt P in einem n-Eck, wenn die Summe aller Abstände von diesem Punkt P zu allen Ecken minimal sein soll. Im Gegensatz zu den meisten weiteren speziellen Punkten im Dreieck existiert der Fermat-Punkt auch in n-Ecken mit der Eckzahl n>3. Es gibt jedoch bisher keine analytische oder geometrische Methode den Fermat-Punkt für n-Ecke mit n>4 zu bestimmen. Das von Andrew Vázsonyi beschriebene numerische Lösungsverfahren kann mit GeoGebra interaktiv eingesetzt und visualisiert werden.
Martin Guggisberg
PH FHNW
Agenda
- Geschichtliche Betrachtung
- Exakte Lösung für n=3
- Numerisches Verfahren für n>3
- Experimentieren mit dem Weiszfeld Algorithmus


"Wo befindet sich ein Punkt P in einem Dreieck, wenn die Summe aller Abstände von diesem Punkt P zu den drei Ecken minimal sein soll."
Dorrie, H. (1965). 100 Great problems of elementary mathematics. Dover Publications.

The Weber problem finds the point in a plane which minimises the sum of weighted Euclidean distances to a set of fixed points.
This is interpreted as finding the factory location which minimises the total weighted distances from suppliers and customers, where weights represent relative volumes of interactions, e.g. weight of material to be transported from a supplier, or volume of finished products for a customer.
Drezner, Z., & Hamacher, H. W. (Eds.). (2004). Facility location: applications and theory. Springer.
Zahlreiche weitere Bezeichnungen
the Fermat problem, the Fermat-Torricelli problem, the Steiner problem, the Steiner-Weber problem, the Weber problem, the Fermat-Weber problem, the weber facility problem, the one median problem, the median center problem, the spatial median problem, the minimum aggregate travel point problem
Exakte Lösung
für n = 3

Mathbuch Band8 LU18

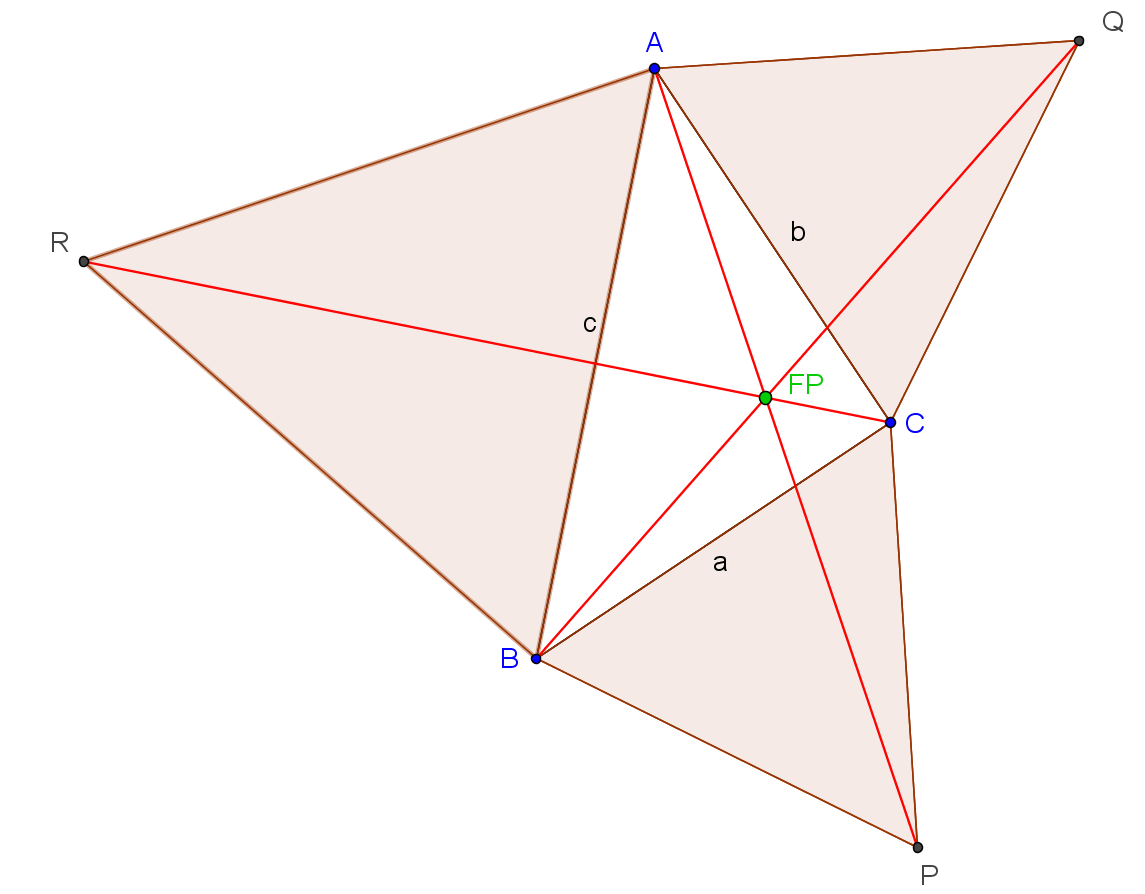
Geometrischer Beweis
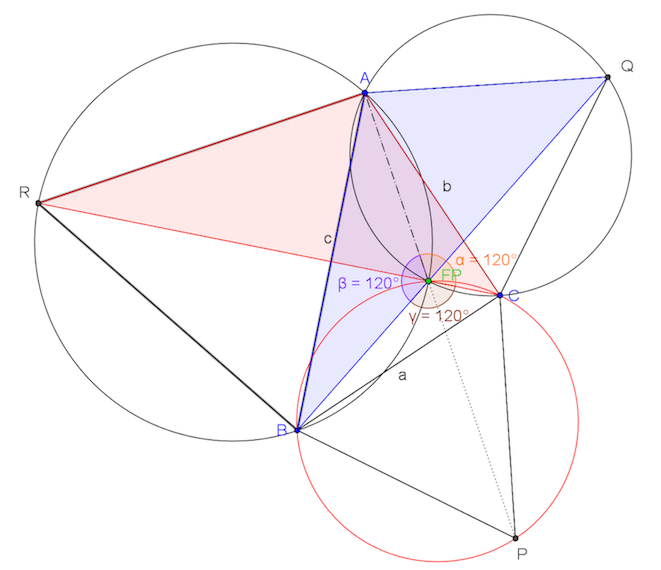
Beweis mit Streckenzug
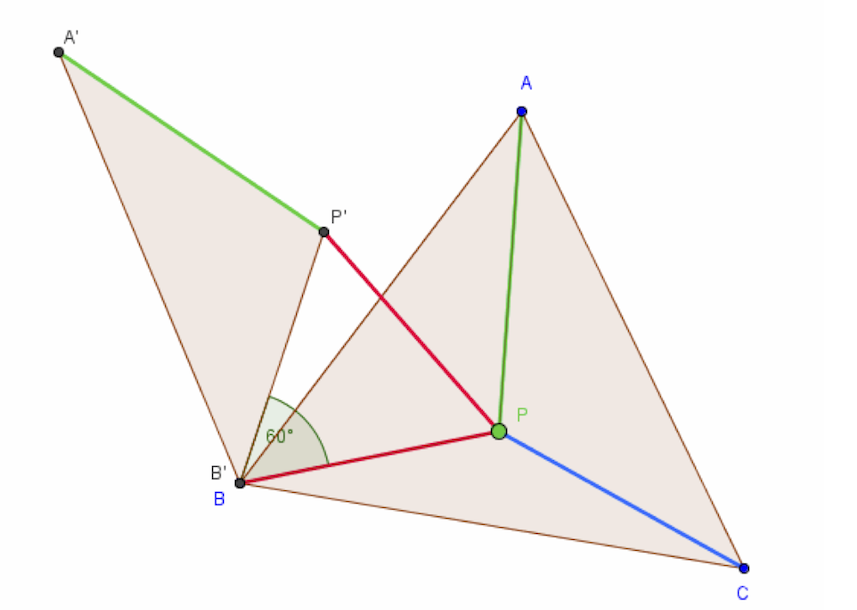
(LU 18, ICT-Zusatzmaterial)
Vorgehen:
Im Dreieck ABC setzen wir irgendwo den Punkt P.
Nun drehen wir das Dreieck ABP um 60° um den Punkt B. So entsteht ein gleichseitiges Dreieck BPP’. Der Streckenzug A’P’PC entspricht nun der Abstandssumme von P zu den Ecken des Dreiecks ABC.
Bewegt man den Punkt P so, dass der Streckenzug A’P’PC geradlinig wird, so hat man die minimale Abstandssumme gefunden.
Weitere Lösungen:
Wer hat als erstes ein numerisches Lösungsverfahren für n>3 gefunden?
Facility Location Problems
Ein Teilgebiet der kombinatorischen Optimierung
1966 findet M. L. Balinksi eine approximative Lösung des Fermat-Weber Problems für n-Ecken.
M. L. Balinksi. On finding integer solutions to linear programs. In Proceedings of the IBM Scientific Computing Symposium on Combinatorial Problems, pages 225–248. IBM, 1966.

I was sixteen when I became intrigued with the N point
problem
Andrew Vázsonyi, 1932
Cosider N points and one more
point, X. Measure the distances between X and the given
points, then add the distances. Find point X so
that this sum is the smallest possible.
Andrew Vázsonyi
I found the point X by using an infinite,
recursive algorithm, a most unusual solution
for a problem in geometry. You start with a
point X0, anywhere, and search for a better
solution.
Andrew Vázsonyi, 1937
The paper "Sur le point pour lequel les sommes des distances de n points donnés et minimum", published in Japan in 1937 under the name Endre Weiszfeld became a classic in the mathematics of location analysis.
Modern Formulierung
Varignon Frame
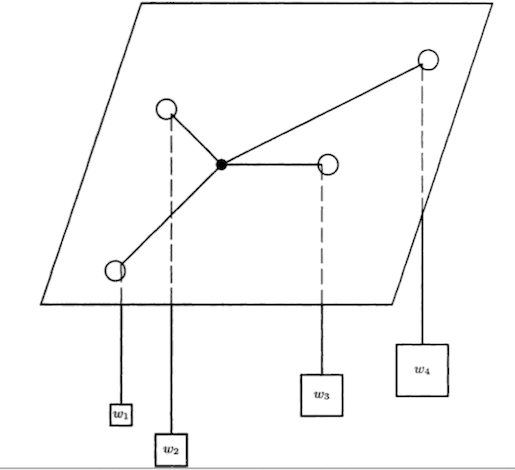
Varignon proposed a mechanical analogue device which has actually been used in practice
Weiszfeld
Algorithmus

by Endre Weiszfeld, alias Andrew Vázsonyi (1916–2003), born in Budapest

Computers have the potential to turn the biggest math-phobe into a math user,
if not a lover.
Andrew Vázsonyi in his book:
Which Door has the Cadillac Adventures of a Real-Life Mathematician
Weiszfeld Algorithmus
Iterative Gewichtung von quadratischen Abweichungen
yk+1=∑Nixi||xi−yk||∑Ni1||xi−yk||
Programming with Python in GeoGeobra (Beta)

Weiszfeld Class
class Weiszfeld(object):
mypoints = None
text1 = None
def __init__(self):
...
def drawPoints(self):
...
def distance(self,A, B):
...
def schwerpunkt(self):
...
def median_approx(self,P, points):
...
def geometric_median(self,points, epsilon):
...
def update(self):
...draw random points
define eventlisteners
class Weiszfeld(object):
def drawPoints(self):
N = int($Anz.value)
xcoords = [random.uniform(3, 17) for i in range(N)]
ycoords = [random.uniform(3, 10) for i in range(N)]
self.mypoints = [Point(x, y,point_size=6, \
color=Color(118,175,236), label_visible=True) \
for x, y in zip(xcoords, ycoords)]
...
for p in Point.all:
p.onupdate=refresh
...
...def refresh(self):
alg.drawSchwerPunkt()
alg.drawFermatPunkt()Using a global object
# GLOBAL VAR
global alg
alg = Weiszfeld()
alg.drawPoints()
alg.update()
$Anz.onupdate=initdeleting all points
for p in Point.all:
p.remove()Calculation Center of mass
def schwerpunkt(self):
x0=y0=0
n = len(self.mypoints)
for P in self.mypoints:
x0=x0+P.x.value
y0=y0+P.y.value
return (x0/n,y0/n)Calculate next interation Position of FP
def median_approx(self,P, points):
"""
Return a new approximation to the geometric median
of `points` by applying one iteration of Weiszfeld's
algorithm to the old appromixation P.
"""
W = x = y = 0.0
for Q in points:
d = self.distance(P, Q)
if d != 0:
w = 1.0 / d
W += w
x += Q[0] * w
y += Q[1] * w
return x / W, y / WMain Loop
def geometric_median(self,points, epsilon):
"""
Return an approximation to the geometric median for
`points`. Start with the centroid and apply Weiszfeld's
algorithm until the distance between steps is less
than `epsilon`.
"""
n = float(len(points))
P = tuple(sum(P[i] for P in points) / n for i in range(2))
while True:
Q = self.median_approx(P, points)
if self.distance(P, Q) < epsilon:
return Q
P = QInteraktiv Programmieren (beta)
Numerische Experimente
Konvergenzverhalten des Weiszfeld Algorithmus
Für n=3 kann ein Winkel von 120° beobachtet werden
Keine Winkelabhängigkeit für n>3
FP bewegt sich auf einem Orbit
FP springt auf innere Punkte
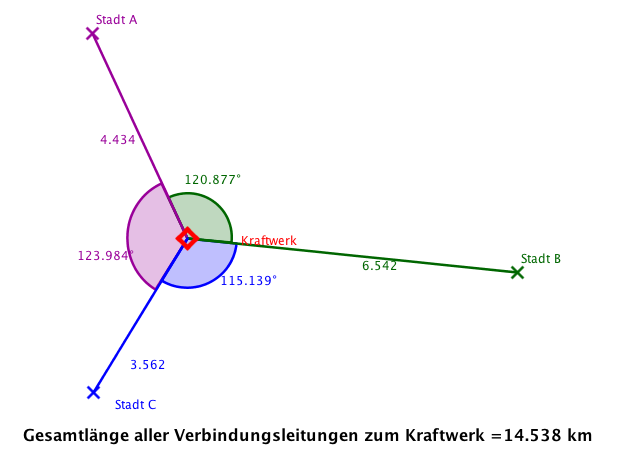
Wo befindet sich der Mittelpunkt von Europa ?
Interactive Demo (JavaScript)
GeoGebra Materials : https://www.geogebratube.org/material/show/id/66049

Demo 2
GeoGebra Materials : https://www.geogebratube.org/student/m66688

weitere Experimente
z. B. Modellierung einer Kamera
Ein perspektivisches Abbildungssystem kann mit Hilfe von Matrizen und homogenen Koordinaten modelliert werden.
P=(10001001/n0), R=(cos(Θ)sin(Θ)0−sin(Θ)cos(Θ)0001)
T=(10Tx01Ty001)
Im Kino
versuchen Agenten in einen Tresorraum einzudringen, ohne dass Sie von einem Wächter entdeckt werden.
Sie projizieren dafür den hinteren Teil eines schmalen Gangs perspektivisch auf eine Leinwand (Bildebene).
Anschliessend bewegen sie die Leinwand langsam nach vorne.
Die Sache fliegt in dem Moment auf, in welchem ein zweiter Betrachter hinzu kommt.
Ausschnitt Mission Impossible 4
Vielen Dank
?
Vortrag, Filme und interaktive Applets sind auf GitHub.
https://mgje.github.io/presentations/