Mathematisches Experimentieren mit „ipython notebook“

Forschendes Lernen in der Sek II

Dr. Martin Guggisberg
Pädagogische Hochschule FHNW
Basel, Schweiz

50. GDM-Jahrestagung Heidelberg 2016

Ausgehend vom arithmetisch-musikalischem Gruppenspiel Ping-Pong (Cslovjecsek, M., PM 42, 2011) wird in diesem Beitrag aufgezeigt, wie Schülerinnen und Schüler der Sekundarstufe 2 mit Hilfe des Werkzeug „iPython notebook“ einzelne Spielsituationen simulieren können und diese anhand spezieller Visualisierungen in verschiedene Kategorien einteilen können. Die Arbeitsweise der Schülerinnen und Schüler entspricht damit dem aktuellen Trend in der Forschung elektronische Notizbücher zu veröffentlichen.

Gliederung

• Mathematisches Experimentieren mit elektronischen Laborjournale
• Exemplarisches Beispiel zum arithmetisch-musikalischem Gruppenspiel Ping-Pong

Experimentieren

Durch Hypothesen geleitetes, planvolles und kontrolliertes Handeln mit Objekten zum Zweck der Erkenntnisgewinnung durch Beobachtung

( Ludwig & Oldenburg 2007)

Experimentieren in der Mathematik

• Mathematik zum Anfassen (Mathematikum in Gießen, Beutelspacher)
• Lernen durch Experimentieren (Ludwig & Oldenburg)
• Mathematics by experiment (Borwein & Bailey)

Mathematisches Experimentieren mit dem PC

A. Engel,Stuttgart : Klett, 1991 Inhalt: Zahlentheoretische Algorithmen, Wahrscheinlichkeit,Statistik, Kombinatorische Algorithmen

Mit dem Computer experimentieren $\to$ Wissenschaftliches Rechnen

Neue Studiengänge Computational Sciences in XXX

Laborjournal

Systematische Aufzeichnung aller inneren und äusseren Paramter, geometrische Konfiguration, sowie die experimentel ermittelten Ergebnisse.

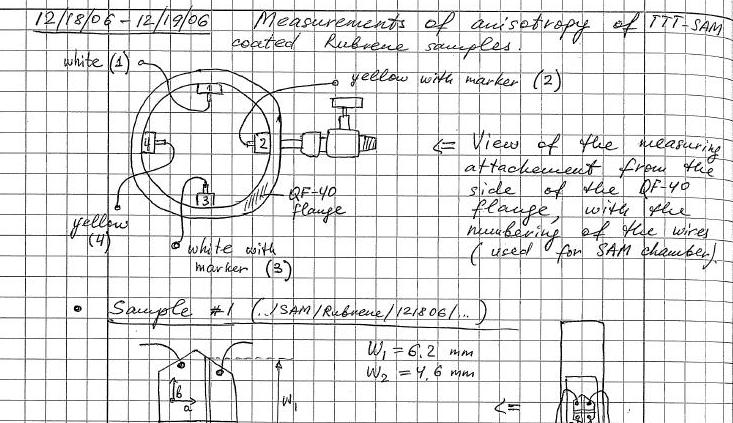
Elektronische Laborjournale

• Automatisierte elektronische Erfassung aller Parameter
• Möglichkeit für interaktive, manuelle Ergänzungen (Figuren, math. Formeln, Texte) $$ \int_0^\infty x^2-x^3-x^4 dx$$
• Werkzeuge zur Datenvisualisierung

Elektronische Laborjournale

direktes Arbeiten in der Cloud

• https://try.jupyter.org/
• https://studio.azureml.net/

nahtlose Verteilung

• Notebook Gallery http://nb.bianp.net/sort/views/
• Beispiele
  • Functional Geometry
  • Discrete Cosine Transform

Voraussetzungen für mathematische Experimente

• Offen Ausgangslage
• Unüberschaubarer Konfigurationsraum

• Beispiele

  • Spiele wie z.B. Schach

  • Naturwissenschaftliche Simulationen

    • Aerodynamics-Hydrodynamics

    • Reaktions-Diffusion-Systeme

    • Angetriebener harmonischer Oszillator

    • Simulation von Schwarmverhalten

    • Statik Simulation

Einsatz von elektronischen Laborjournalen an der Hochschule

• Lehrerausbildung Masterkurs Wissenschaftliches Rechnen
• EU Forschungsprojekt: "European Music Portfolio - Maths: Sounding ways into Mathematics"

 Ping-Pong Aktivität

Das Ping-Pong Spiel behandelt eine koordinative, kooperative, rhythmische AufgabensteIlung, welche mit Gruppen von 4 bis 26 Schülerinnen und Schülern durchgeführt werden kann.

Cslovjecsek, M., Guggisberg, M. & Linneweber-Lammerskitten H. (2011). Mathe macht Musik Ping-Pong, PM Praxis der Mathematik 42 (pp. 13 – 18).

Spielregeln:

• Die ganze Klasse sitzt im Kreis.
• Dazu wird der Reihe nach fortlaufend gezählt (1,2, 3, 4 ...).
• In einem ersten Schritt werden alle Dreier-Zahlen (3, 6, 9, 12, 15 ...) mit dem Wort "Ping" ersetzt.
• Analog werden dann die Vierer-Zahlen (4, 8, 12, 16 .. .) mit ,,Pong" ersetzt.
• Nach einigem Üben kann versucht werden, die Dreier- und Vierer-Zahlen gleichzeitig zu ersetzen (12, 24 ... heißt dann Ping-Pong ).
• Viel Übung ist erforderlich, wenn bei Ping und Pong als zusätzliche Regel ein Richtungswechsel vorgenommen wird

Spiel mit Ping = 3 und Pong = 4

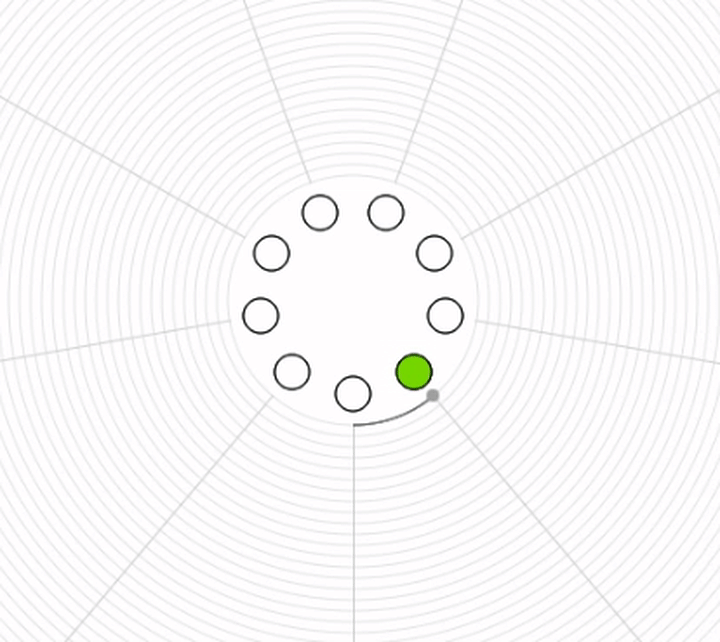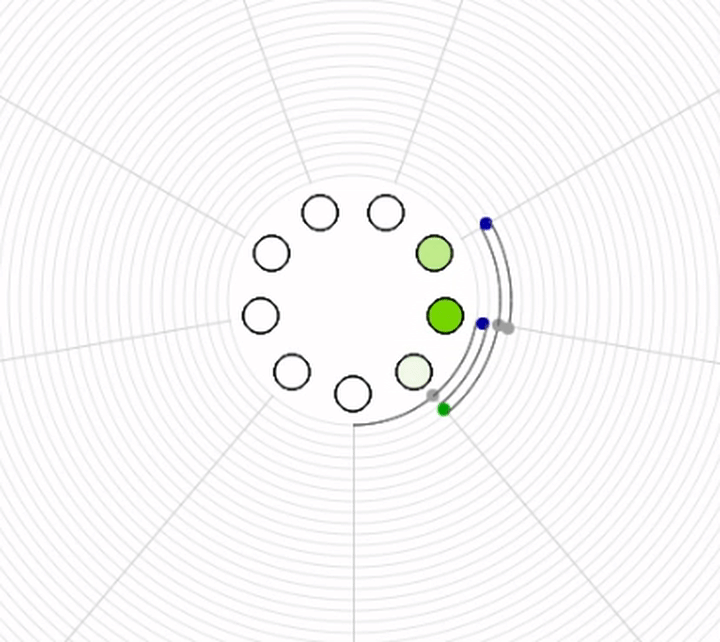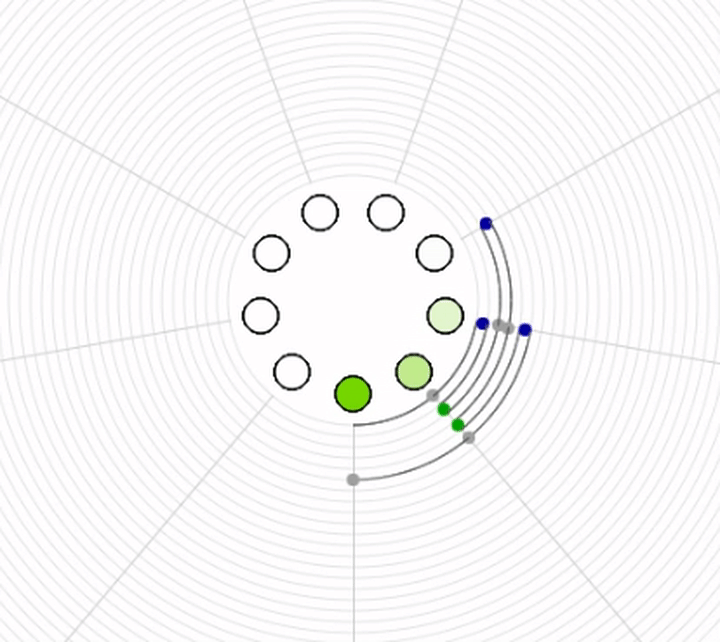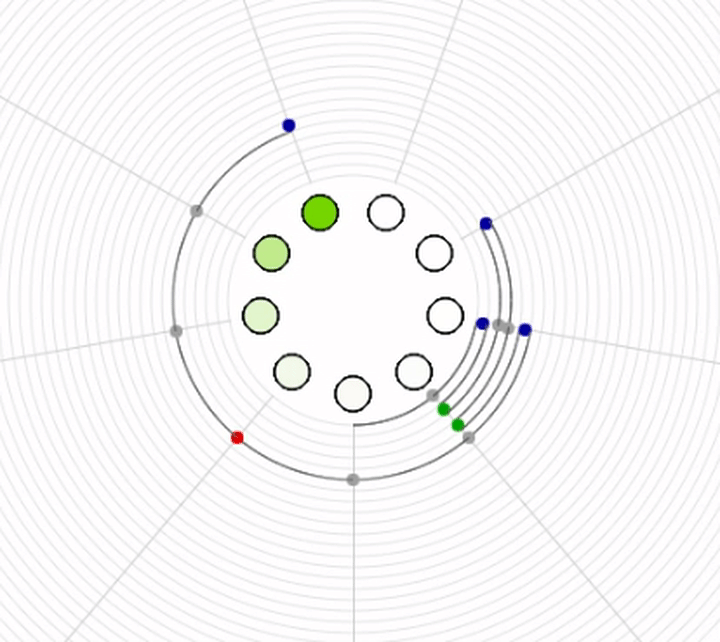
Was muss ich sagen, wenn ich an die Reihe komme ?

Welche Zähl-Zahlen treten bei meiner Spielposition auf ?

Gibt es eine Partitur für dieses Spiel ?

Durch Abzählung zur Lösung

$\mathbb{N} \times \mathbb{N} \times \mathbb{N} \to \mathbb{Z}$

$(n, \mbox{Ping-Zahl}, \mbox{Pong-Zahl}) \mapsto \mbox{Spielposition}$

Verschiedene Darstellungen des Spielverlaufs

für ping = 3 und pong = 4

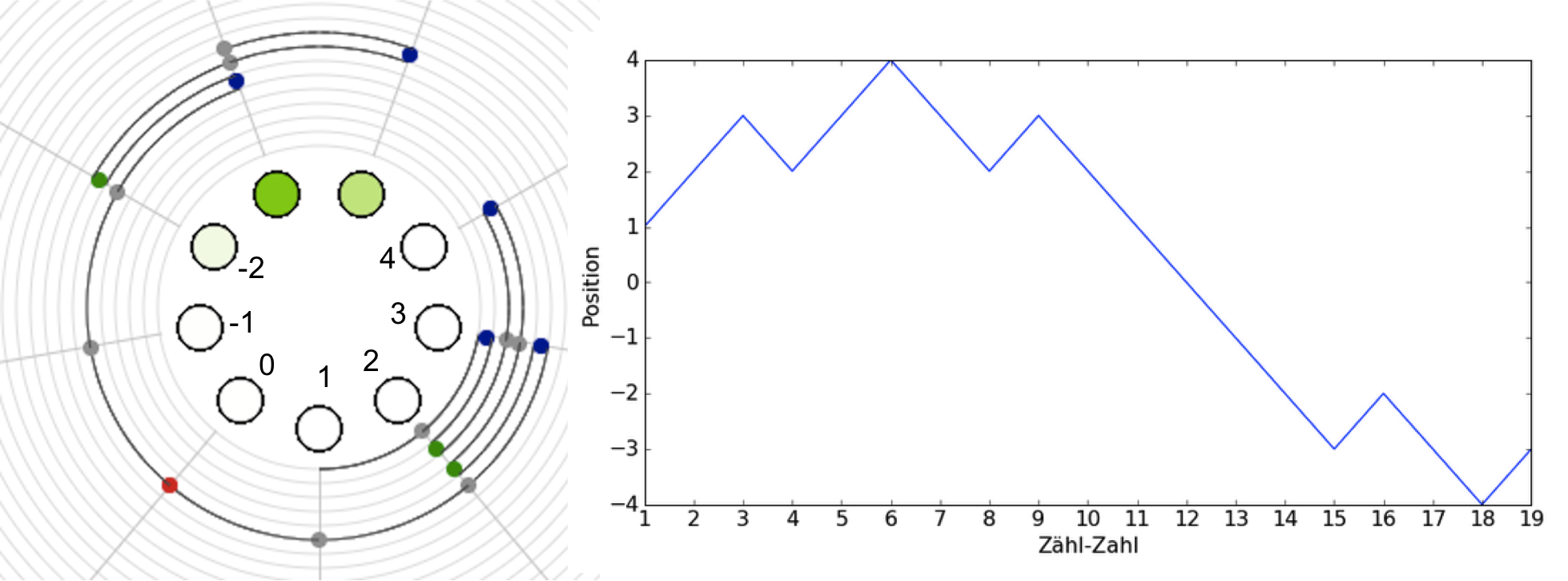
Durch Abzählen zur Lösung (Python Programm)

def pingpong(n, ping=3, pong=4):
    p = 0
    # Zählschritt (1 oder -1)
    step = 1
    # Zählen von 1 bis n
    for i in range(1,n+1):
        p = p + step
        # Vergleiche Zähl-Zahl mit ping und pong 
        # falls genau eine Bedingung zutrifft (xor) 
        # -> ändere die Richtung (XOR) 
        if bool(i%ping)^bool(i%pong):
            step *= (-1)
    return p

pingpong(4)

2

Pseudo-Code Ping-Pong zur Berechnung der Spielposition

p = 0
step = 1
for i : 1 .. N do
    p = p + step
    if (i mod ping) xor (i mod pong)
        step = (-1)* step
return p

Spielpositionen für die ersten 30 Zähl-Zahlen

y = [pingpong(n) for n in range(1,31)]
print y

[1, 2, 3, 2, 3, 4, 3, 2, 3, 2, 1, 0, -1, -2, -3, -2, -3, -4, -3, -2, -3, -2, -1, 0, 1, 2, 3, 2, 3, 4]

Visualisierung des Spielverlaufs mithilfe eines Zähl-Zahl-Position-Diagramms

%matplotlib inline
import numpy as np
from matplotlib.pyplot import *
def init_plot():
    fig = figure(figsize=(12, 6))
    yticks(size=16)
    xticks(size=16)
    xlabel(u'Zähl-Zahl',fontsize=16)
    ylabel('Spielposition',fontsize=16)
    k = len(y)
    #xlim([1,k-1]) 
    #xticks(np.arange(1, k, 1.0))
    

/Users/guggisberg/Library/Enthought/Canopy_64bit/User/lib/python2.7/site-packages/matplotlib/font_manager.py:273: UserWarning: Matplotlib is building the font cache using fc-list. This may take a moment.
  warnings.warn('Matplotlib is building the font cache using fc-list. This may take a moment.')

init_plot()
xticks(np.arange(0,len(y),5),np.arange(1,len(y),5),size=16)
plot(y)
'Spielverlauf ping=3 , pong=4'

'Spielverlauf ping=3 , pong=4'

Abhängigkeit von Ping- und Pong-Zahlen

## Abhängigkeit von Ping und Pong
ping = 3
pong = 5
y = [pingpong(n,ping,pong) for n in range(1,600)]
init_plot()
plot(y)
'Spielverlauf ping=%d , pong=%d' %(ping,pong)

'Spielverlauf ping=3 , pong=5'

Weitere divergente Konfigurationen

y = [[pingpong(n,3,pong) for pong in range(5,12,2)] \
     for n in range(1,200) ]
init_plot()
plot(y)
#legend(('ping=3,pong=5','ping=3,pong=7','ping=3,pong=9','ping=3,pong=11'))
'Spiele (ping=3,pong=5),(ping=3,pong=7),(ping=3,pong=9),(ping=3,pong=11)'

'Spiele (ping=3,pong=5),(ping=3,pong=7),(ping=3,pong=9),(ping=3,pong=11)'

6 Perioden

ping=4
pong=16
init_plot()
y = [pingpong(n,ping,pong) for n in range(1,6*ping*pong)]
plot(y)
'Spielverlauf ping=%d , pong=%d' %(ping,pong)

'Spielverlauf ping=4 , pong=16'

Ping-Pong Parameter Karte / Spielposition in Abhängigkeit von Ping und Pong

def plot_maps(zmin,zmax):
    n_col = 4
    n_row = 3
    dn = 50
    figure(figsize=(2.6 * n_col, 2.6 * n_row))
    subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.35)
    for i in range(1,n_row * n_col+1):
        subplot(n_row, n_col, i)
        title('n='+str(int(i*dn)))
        imshow( [[pingpong(i*dn,k,l) for l in range(2,41)] for k in range(2,41)],vmin=zmin,vmax=zmax)
    colorbar()

""

''

plot_maps(0,1200)

import numpy as np

def plot_map_n_12347(zmin,zmax):
    ymap = [[pingpong(12347,k,l) for l in range(2,41)] for k in range(2,41)]
    fig = figure(figsize=(12, 8))
    xticks(np.arange(0,40,5),np.arange(2,40,5),size=16)
    yticks(np.arange(0,40,5),np.arange(2,40,5),size=16)
    imshow(ymap,interpolation="nearest",vmin=zmin,vmax=zmax);
    colorbar()
    'Parameter Karte ping = 2..40 , pong = 2..40'
    

plot_map_n_12347(0,11000)

divergente Fälle: (2,6);(3,9);(4,12);(5,15)
(2,10);(3,15);(4,20)

Wertebereiche auf -500 .. 500 einschränken

plot_map_n_12347(-500,500)

Betrachtung von Fälle ping > 35, pong > 36, nahe bei der Diagonalen

(39,40) , (39,38) , (39,36) (37,40) , (37,38) , (37,36) (35,40) , (37,38) , (37,36)

init_plot()
legend((('p33:40', 'p35:40', 'p37:40', 'p39:40')))
y = [[pingpong(n,ping,pong) for ping in range(35,41,2) for pong in range(36,41,2)] for n in range(1,2800) ]
leg= [str(str(ping)+':'+str(pong)) for ping in range(35,41,2) for pong in range(36,41,2)]
plot(y)
legend(tuple(leg))
'Spielverlauf (35,36) , (35,38) , (35,40) , (37,36) , (37,38) , (37,40), (39,36) , (39,38) , (39,40)'

'Spielverlauf (35,36) , (35,38) , (35,40) , (37,36) , (37,38) , (37,40), (39,36) , (39,38) , (39,40)'

Kombinationen von ungeraden und geraden teilerfremden Paare scheinen periodisch zu sein

Mit einer Periodizität von $2 \cdot ping \cdot pong $

Und einer Amplitude von $ \approx \frac{32}{125} \cdot ping \cdot pong $

ping = 41
pong = 42 #Torsten
init_plot()
y = [pingpong(n,ping,pong) for n in range(1,4*ping*pong) ]
plot(y)

'Spielverlauf ping=%d , pong=%d' %(ping,pong)

'Spielverlauf ping=41 , pong=42'

Vergleich einer normalisierten Ping-Pong Kurve mit einer Sinus Funktion

import numpy as np
from math import pi

def fitPingPong(ping,pong):
    Amplitude = 32.0 / 125 * ping *ping
    x = np.linspace(0,4*pi,4*ping*pong-1)
    y = np.array([pingpong(n,ping,pong)/Amplitude for n in range(1,4*ping*pong) ])
    y2 = np.sin(x)
    return x,y,y2

x,y,y2 = fitPingPong(41,42)
init_plot()
plot(x,y,'-',x,y2,'-')
legend(('Spielverlauf','f(x)=sin(x)'))
'Approximation von sin(x) durch normalisierten Spielverlauf (41,42)'

'Approximation von sin(x) durch normalisierten Spielverlauf (41,42)'

Potenzial von elektronischen Laborjournalen

• Abzählung von Möglichkeiten
• Numerischen Berechnungen
• Visualisierung von Phasenräumen

• interaktiv - direkt im Browser lauffähig

• Kann als Präsentationswerkzeug verwendet werden

• 100% Open Source

Mögliche Themenfelder

• Numerik
• Mechanik
• Thermodynamik
• Populationsdynamik
• Informatik

Mathematiker wie z.B. Fermat, Gauß, Euler oder Riemann haben viele Stunden ihres Lebens damit verbrachten, Rechnungen im Kopf durchzuführen, um „mögliche Wahrheiten“ zu erkunden.

Mögliche Themen für Schuluntericht (Sekundarstufe II):

• Entdecken durch Abzählen

  • Konvergenz von Folgen und Reihen
  • Berechnung von Wahrscheinlichkeiten
  • Approximation spezieller Zahlen

• Entdeckung durch Visualisierung

  • Verhalten von Funktionen
  • Symmetrien in der Ebene

• Experimentelle Untersuchung von Daten

  • Suche nach Gesetzmässigkeiten (Regression, Methode der kleinsten Quadrate)
  • Untersuchung von Korrelationen

Vielen Dank !

Alle Materialien sind auf github

Dieses elektronische Laborjournal finden Sie auf

https://github.com/mgje/PIUMP

Vortrag: Sounding Ways into Mathematics

Do 10.3. 8:15-9:00 Uhr Ort: A125

Musikalische Zugänge zur Mathematik – Sounding Ways into Mathematics

Andreas Richard, Markus Cslovjecsek